线性回归的假设检验
亲爱的朋友们,我们在日常生活中,经常会遇到需要检验假设成立的情况(才不是啊喂!)。
这里我简要记录下我学习三种假设检验方式,即lagrange multiplyer test, likelihood-ratio test 与 wald test的一些记录,希望能够帮到又需要的人
线性回归的检验
模型
假设回归的模型为\(Y=\alpha + \beta x + \epsilon\)
0假设为x于y是uncorrelated,进行回归之后,\(\hat{\alpha}\)和\(\hat{\beta}\)作为截距和slope被计算出来,\(SE_{\hat{\beta}}\)是各个点对于line的standard error。之后计算\(\hat{\beta}\)的t值:
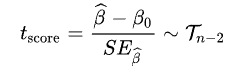
服从自由度为n-2的t-distribution,
其中slope coefficent的standard error是
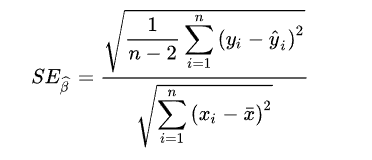
就是用y的偏差值(自由度为n-2)用x的方差进行归一化
样本的标准差被计作s,就是根号下除以n-1的那个,这样计算出来的样本标准差是整体标准差的无偏估计,也就是\(E(s)=\sigma\),这个操作叫作bessel‘s correction
bessel’s correction
$$
\sum_{i = 1}^n (x_i - \bar{x}) ^ 2 = \sum (x_i^2 - 2x_i\bar{x} + \bar{x} ^2) = (\sum x_i^2) - 2n\bar{x}^2 + n\bar{x}^2 = \sum x_i^2 - n\bar{x}^2
$$
$$
E(☝) = \sum E(x_i^2) - n E(\bar{x}^2) = \sum (var(x_i) + E(x_i)^2) - n (var(\bar{x}) + E(\bar{x})^2)
$$
其中,
$$
var(x_i) = \sigma, E(x_i) = \mu, E(\bar{x}) = \mu, var(\bar{x}) = \sigma/n
$$
所以上边的等于\(\sum_{(1..n)} (\sigma + \mu^2) - \sigma - n \mu^2\)
两个\(n\mu^2\)消去,剩下一个\((n-1)\sigma\).
所以\(\sum_{i = 1}^n (x_i - \bar{x}) ^ 2\)要除以n-1才是\(\sigma\)的无偏估计
假设检验,以t-test为例
假设检验的目的:
- 双样本检验:检测两个随机变量是不同的,它先从两个随机变量里面各自抽取一些样本,然后对这些样本进行假设检验,这就是two-sample t-test,比如随机分组100个病人到治疗和对照组里面。
- 单样本检验:student-t这个统计量就是把观测量进行“正规化”,也就是用样本均值减去整体均值,除以(样本方差/根号n,n是样本个数)。分母这部分又叫作mean的standard error,是一个statistic的样本的标准差除以根号n。它假设\(\bar{x}\)也就是样本均值服从以\(\mu\)为均值,\(\sigma^2/n\)为方差的normal distribution,检验这个t统计量是否\(~\mathcal{N}(0, 1)\)
Wald test
未完待续...