PID controller 入门视频
入门视频是这一系列的视频:
Understanding PID Control, Part 1: What Is PID Control?
PID 是三个词的缩写:propotional, integral and derivitive。着三个components都以当前被控对象和目标的差值作为输入,输出分别对应着对被控对象的当前误差x,当前误差的变化速率dx和误差的历史状态\(\int dx\),最终输入的控制信号就是着三个的线性组合
饱和信号 (saturation)
这时候就有一个问题,现实的actor与输入信号并不是线性的,首先我们关注saturation效应,比如电机不能无限提高转速,这时就需要在输入信号输入到actor之前进行一个saturation check,先检查想要输入的信号是不是超过了上限,如果是,并且误差和控制信号同号,那么就关闭误差-积分器这一通路(把积分器的输入设置为0),以停止对误差进行积分,从而避免输入一个过大的信号。这时候保证1.如果已经wind up了,那么积分器的输出是平的(因为在这一段是对0进行积分),2.如果误差变号了,那积分器的输出立马减小
de-noising,使用derivative和low-pass+derivative,也就是filtered derivative
使用有cutoff frequency的filter,在derivative之前,使用first-order low-pass filter(此处基于laplacian domain transfer function, cheetsheet see below:)
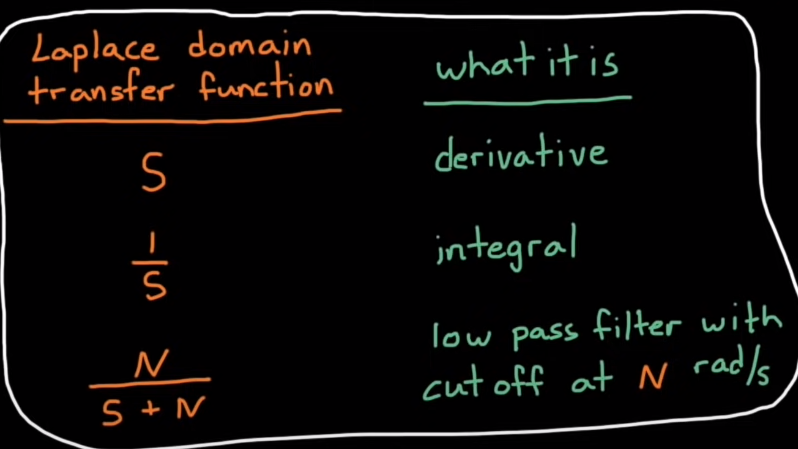
回忆:一个信号先通过低通再通过derivative,在时域上体现为卷积,在S域上体现为两个组分的成绩,这两个的串连等效于在正向的一个乘以N的forward path,加上一个1/s的feedback path
考虑正弦函数\(y=Asin(\omega x + \phi)\),它的导数的最大幅度正比于它的频率,但我们想让它在某个cut-off频率后边的噪声都被block掉,以至于高频的噪声对于derivative分量不造成过大的影响,就需要在dirivative之前加一个滤波器,这也就成了filtered derivative
pid tuning
- is the system well-behaved? it’s not, because it’s:
- highly nonlinear
- open-loop unstable
- lots of delays
- non-minimum phase
一个实际的pid系统的例子,以示例pid tuning
assume 一个dc-motor,电压越高,转速越快,给系统一个步进电压,电机会在一个delay之后逐渐提高转速直到一个稳定的转速
第一种方式,derivede from the 1st principle
用类似于lagrangian equation等列出电机的运动方程,这种情况是“white box method”,因为知道所有系统的细节,更常见的方式是知道系统有什么components,比如知道电机有inertia,有friction正比于angular speed,但是并不知道它们具体的大小,这种情况叫做“grey box method”,这种情况或者用testing的方式,或者用system identification的方式来确定参数
第二种方式,当系统太复杂不能从1st principle导出时
这里主要是用system identification的方式,这种方式并不要求你对系统的所有动力参数有好的理解,只是对输入-输出进行研究来推断model,通过模拟输入输出来的到一个线形的近似系统,然后在这个线性系统上进行tuning。
或者直接进行linearization,对复杂非线性系统线性化,这比system id的方式更方便debug和更可靠
用控制论来tune pid
所有的pid,写成S域的都是如下形式:
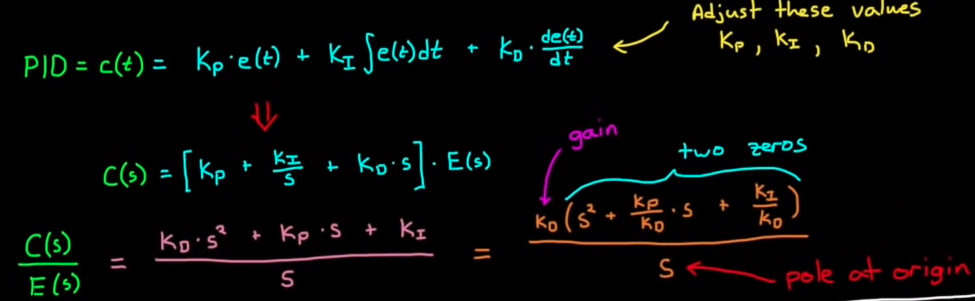
一个pole在源点,所有的pid设计都是怎样放置两个零点。
但是一般都不会直接用dirivitive,而是用filtered dirivitive(de-noising,使用derivative和low-pass+derivative,也就是filtered derivative),这样就引入了一个额外的pole
两种方式,一个是pole placement,一个是loop shaping