Multi-arm-bandit学习笔记
与其说KL-LUCB算法是用来解决K-臂老虎机,不如说它是用来解决抛K个不均匀硬币问题,因为它要解决的实际上是对K个不相关的伯努利分布的独立事件收益的问题,
考虑\(X_i \sim Bernoulli(p_i), 1\leq i \leq K\)为K个独立不相关的伯努利事件(K个不均匀硬币),每枚硬币head是收益+1,tail是没有收益,问在抛出t次的时候,如何确定收益最高的m个硬币
经典multi-arm-bandit问题:
考虑经典的老虎机(非伯努利分布),m=1时候几种经典做法:
-
exploration only:
每个都搂t/K次,缺点是没有利用“所有老虎机平均收益不同”的特点
-
exploition only:
每个都搂一次,剩下的选择收益最高的一个完了命地搂,缺点是采样个数最小
-
\(\epsilon\)-greedy:
在前\(\epsilon/t\)的次数中,平均搂各个arm,然后找出均值最高的一个完了命的搂
-
0-regret:
这是最理想的情况,你知道哪个平均收益最高,然后玩了命地搂,一切算法都要尽量压低自己的收益和0-regret情况之间的差距
explore-m(选择m个最好的)硬币问题:
考虑\(X_i \sim Bernoulli(p_i), 1\leq i \leq K\)为K个独立不相关的伯努利事件(K个不均匀硬币),每枚硬币head是收益+1,tail是没有收益,问在抛出t次的时候,如何确定收益最高的m个硬币
-
exploration only:
平均每个都抛同样的次数,选出收益最高的m个
-
racing algorithm:

每次把剩下的所有arms搂一遍(sample all the arms in R),更新各arm的confidence interval的上下界
把剩下的所有arms分成收益最好的m-|S|个(\(J\)集合)和剩下的收益最差(\(J^c\)集合)的,S是上一轮已经选出来“胜出race”的arms
如果R集合最差的arm过于拉胯,把它放进discard(D)集合中,或者如果R中最好的arm过于牛逼,那么就把它放进S(select)集合中
“R集合最差的arm过于拉胯”,体现在R集合中平均收益最低的那个arm(\(a_w\),即worst arm)的上界,甚至比J集合下界最低的arm的下界还低(with a margin of \(\epsilon\))
“R集合最好的arm过于牛逼”,体现在R集合中平均收益最高的那个arm(\(a_B\),即best arm)的下界,甚至比\(J^c\)集合上界最高的arm的上界还高(with a margin of \(\epsilon\))
然后选择到底是worst arm的拉胯程度更夸张还是best arm的牛逼程度更夸张,选择更夸张的那个arm加到S(best arm)或者D(worst arm)中
重复,直到S中有m个arms
这个算法的问题是,“每次把剩下的所有arms都搂一遍”这里sample complexity太高了,完全可以有针对性地做adaptive sampling,所以有了LUCB:
- LUCB:

这个算法里面除了第一次对所有arm搂一遍,计算各自的confidence上下界以外,其它次数都只搂ut和lt,也就是\(J^c\)(潜在被抛弃)集合中上界最高的arm,和J(潜在接受)集中下界最高的arm。因为这两个arm是最有可能被分错的。
搂这两个arm之后,可以更新这两个arm的平均收益,所以可以更新J集合和ut与lt,之后再更新B,这个代表两集合之间的含混程度,小到一定范围就可以停止了
所有这些算法里面还留了一个问题就是confidence bound(上下界)怎么计算,从race到原版的LUCB都是用的Hoeffding bound,就是
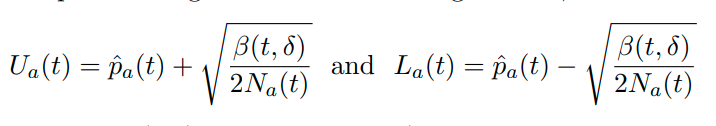
\(\hat{p}_a(t)\)代表arm a在t时刻的平均收益,\(N_a(t)\)是a在t时刻搂的次数,\(\beta(t,\delta)\)是explore parameter
但是KL-LUCB就是用KLD来计算这个上下界:
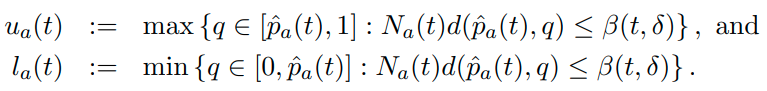
其中d就是KLD,其它参数同上,可以由Pinsker’s inequality证出来
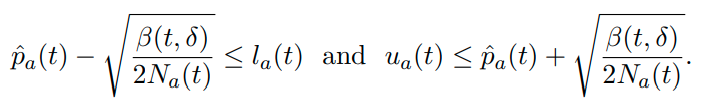
也就是基于KLD的上下界比Hoeffding上下界要窄(反正我没证出来,但它在appendix中据说证出来了,那就是证出来了吧)
所以可以使用KLD上下界来更新每个arm的上下界