红黑树复习
亲爱的朋友,你在幼儿园小班学习《算法导论》的时候,是否有过这样的感慨:
网上的红黑树资料要么说得不像人话,要么漏洞百出,或者根本连实现代码都没读懂就大放厥词。
这有可能是我们的检索能力没能跟上网络内容的增殖,也可能是因为网络信息增长的速度可以轻易超过光速*。
所以根据Torvalds的实现,借用这篇的图片,写一下这个总结。
静态性质
红黑树,为满足以下几条性质的二叉排序树:
- 根节点一定是黑的
- 一个红色的父亲要有两个黑色的儿子
- 从根到任意叶子节点的路径需要经过等个数个黑色节点
- 不能有两个相连的红色
另外还有“虚拟叶子节点都是黑的”这个性质,这个只在删除黑节点并维护的时候有用
顺口溜:
根黑各路黑点等
红父黑子红不连
动态性质
插入
新插入的节点应该是红色,按平衡二叉树的方式插入,唯一有可能违反的就是“不能出现连续两个红色”的规则,即插入后父节点也是红色,这时候兄弟节点和祖父节点必是黑色,唯一的变量是叔节点,对叔节点分情况讨论
- 叔节点为红色(下放-递归):爷爷的黑色下放到父节点和叔节点,爷爷变红,此时爷爷和太爷爷有可能违反连红原则,聚焦爷爷节点,修复爷爷和太爷爷之间的规则违反情况
- 叔节点为黑色(转1~2次,改色):先以自己-父亲为轴,往远离叔节点的方向转,再以自己-原来的爷爷现在的爹节点为轴往靠近原来叔节点方向转,再把自己涂黑,原来的祖父涂红:
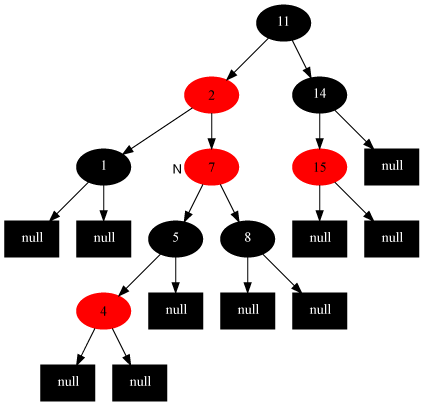
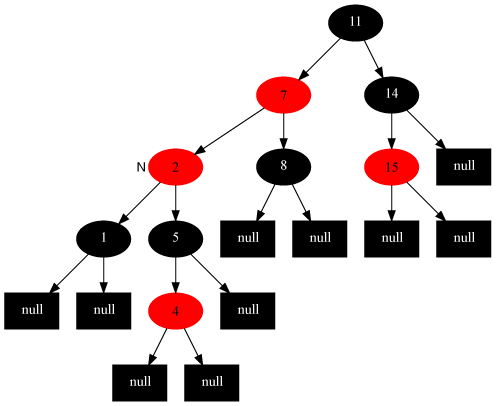
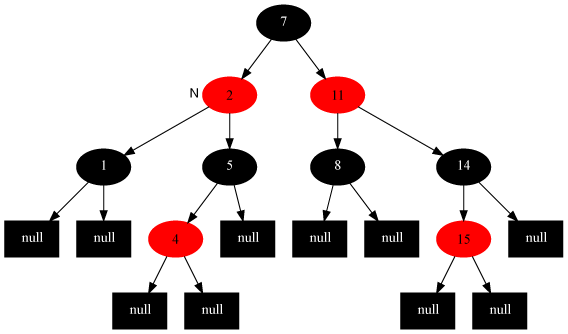
删除
永远只删除叶子节点,如果要删除的不是叶子节点,则持续把自己和自己的最近后继交换,颜色保持不动,不随数据的交换而交换,最后一定会把自己换到叶子节点去,然后再删除
如果最后要删除的叶子节点为红色,那直接删除,不会有什么问题
如果最后要删除的叶子节点为黑色,那进入维护过程,注意在维护过程的循环/递归中,当前关照点(永远是黑点,就算最后删除的是叶子节点,那也是把虚拟的黑色叶子节点作为关照点)的黑点数始终比其它路经少1,目的就是要把这个路经上加一个黑点。所以循环/递归的最后一步一定是把一个之前是红色的节点涂成黑色的。分情况讨论:
- 爹无所谓兄弟黑,侄子都是黑:如果爹是红的,交换爹和兄弟的颜色,“我(N)”把兄弟支的黑S接到爹p上了,兄弟支不损失黑点,我还白嫖了一个黑点,退出维护;如果爹是黑的,那把爹当成下一轮循环的关注点,继续

- 爹无所谓兄弟黑,距离我近的侄子红,另一个黑(这种情况不能以3.的方式一个旋转解决,因为远侄子没法再承载一个黑了):绕着红侄子-兄弟往离我远的方向转,再绕着新兄弟-爹为轴朝向我转,新爷爷变爹的颜色,新爹变黑。这里我白嫖了新爹的黑色,新兄弟(原来的左侄子的左儿子)一支的黑色加点从原来的兄弟变到了新爹

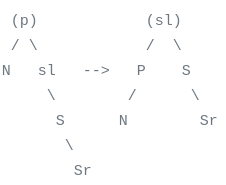
- 爹无所谓兄弟黑,距离我远的侄子红:交换爹和兄弟的颜色,把距离我远的侄子涂黑,绕爹-兄弟向我方向转。我白嫖了原兄弟的黑色,而原来的远侄子自己加了一个黑色

- 爹黑兄弟红(侄子必都黑):绕着爹-叔旋转,交换爹-叔颜色,这里并没有改变我这支的黑点数,所以要继续看新侄子的情况,如果新侄子都黑,则到情况1.;距离我远的侄子红就到3.;如果距离我近的侄子红就到2.

*:光速是狭义相对论下,我们这个宇宙内信息传递的速度,这里只不过是在说网上得内容增长得很快,却没什么信息