也谈softmax(施工中)
引言
随着机器学习的异常火爆,学习它的人也如雨后春笋一般冒了出来,作为时刻保持在时代前沿的Ghost自然也没能免俗跟着一起跳进了大坑,今天不说别的,就着青梅煮酒,我胡扯一点关于机器学习中极为重要的一个函数:softmax
softmax是什么?
softmax是一个函数,它的定义域为\(\mathbb{R}^d\),值域为\((0,1)\),d个输入是数据源的自变量,输入是多个自变量的值,输出是当前输入值应该归到哪一分类的概率。我们先来和它混个脸熟:
例如针对某个三分类两个参数的问题,数据分类为1的概率画出来长酱婶:
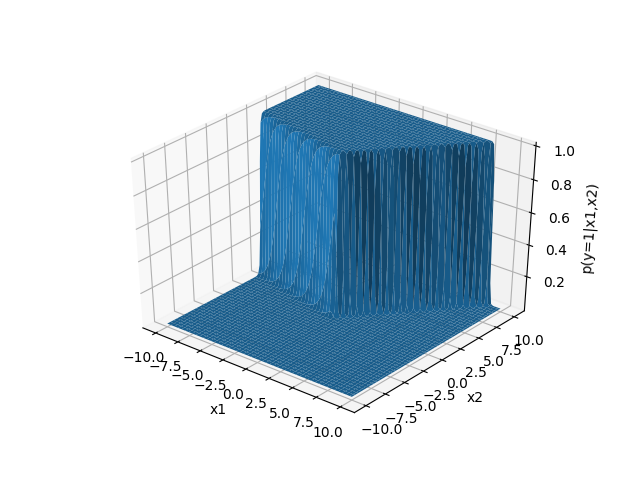
可以看到图像中有一个泾渭分明的界限,左上方概率极为接近1,右下方概率极为接近0,这就是在w的这一特殊配置下,参数空间与分为第一类label的概率关系。softmax公式左边的\(P(y=i|\vec{x})\)表示“在我的输入数据是\(\vec{x}\)的时候,把这个数据分到第\(i\)类中的概率”; 右边的式子比较吓人,咱们一点一点来分析。
先看分子,注意分子上\(\vec{w}\)的下标和预测的y,我们不妨称呼分子为“当前数据点分到i分类时的适合程度”,简称“i适配度”。分子的式子本身由于是自然指数函数,是对\(x\)单调的,也就是说它相当于把原来相对“均匀”地分布在\(\vec{x}\)所在空间中的各个数据点分配了一个“i适配度”,\(\vec{x}^{\, T}\vec{w_i}\)越大的项“i适配度”也就越大,而w则是用来线性调整\(\vec{x}\)的“权重”。到这里可能有人会问,我们已经有一个线性权重了,为什么还需要再套一层幂指数呢?由于一方面仅仅使用线性的权重,难以拟合一些比较复杂的函数;另一方面由于人类认知能力本来就是非线性的,例如给出两组数据,0.6与0.8; 0.7与0.9,问与1的一个“主观距离”,如果是我的话会觉得0.6、0.8一组距离1都“差着不少”;但0.9,就与0.7迥然不同,已经“非常接近”1了。而要让计算机理解这种“感觉”,我们可以巧妙地使用\(e^0.6\)、\(e^0.8\)和\(e\)比较,再用\(e^0.7\)、\(e^0.9\)和\(e\)比较,这样一来就可以直接使用数值差的绝对值来表示这种“感觉”,也就是把正分类和副分类的差距进一步拉大了。
再看分母,分母这个形式有个特定名称叫做“配分函数(Partition function)”,话说这个奇怪的名字我一直觉得就是为了符合音译而硬出来的…………它的作用是遍历加和所有\(M\)个分类的“适配度”,看看分子所对应的第i个分类到底能不能在所有可能分类中“脱颖而出”。并且分母相当于一个正则化因子,它让所有的\(P\)都能被真正视作一个“概率”,即\(\forall i: 0<P(y=i|\vec{x})<1\)并且\(\sum_{i=1}^{M}P(y=i|\vec{x})=1\)
softmax的来历
softmax函数源自物理系四大神课之《热力学与统计物理》(另外三门传说是《经典力学》《量子场论》和《电动力学》,排名不分先后)。里面有一种分布叫做Boltzman distribution,又名Gibbs distribution,它首先由奥地利物理学家路德维希玻尔兹曼于1868年在研究统计物理学中气体热分布的时候提出,随后玻尔兹曼投入大量精力为自己的理论辩护,也因此与他在奥地利的同事交恶。即便如此,这位天才作为讲师在维也纳教授的物理学与哲学课程皆大受欢迎,在大学一度达到万人空巷的程度。但这也没能阻止躁郁症对这颗出色大脑的折磨,玻尔兹曼最终在1906年9月5日于度假中情绪失控,自缢身亡。在玻尔兹曼陨落后人们为了纪念他的卓越贡献,将著名的玻尔兹曼熵公式$S=k\dot ln W$刻在了他的墓碑上。在1902年,美国科学家约西亚威拉德`吉布斯与玻尔兹曼共同创立了统计力学理论,并将玻尔兹曼分布,或吉布斯分布进一步发扬光大。这一概率分部的式子长这样:
其中:
\(\epsilon_i\)表示单个单元的能量,或指系综(系统的集合)能量的一种分布方式;
\(k_b\)是玻尔兹曼常数,\(k_b=1.38064852(79)\times 10^{-23}JK^{-1}\);
\(T\)是热力学温标。
Boltzman分布有两种用途,一是用来描述在一个正则系综(即与大热池等温的若干系统的集合,系统之间没有粒子与能量交换)中,系统能量的分布为\(\epsilon_i\)的概率; 或者另一种用途,是描述一个等温体系下,测量出能量为\(\epsilon_i\)粒子的概率。
当初奥美两国两位巨匠为描述现实世界搭建的巧妙模型,时隔百年又重新站到了时代的前沿,就中波折难免令人唏嘘。
softmax的性质
小时候看大牛Matrix67的博客,他的“特例分析法”让人眼前一亮,就是把要研究的对象尽可能地加以约束,先放到直观能够“观看”的程度,同时尽可能地不损失对象的一般性,随后再用类似数学归纳的方法来引申出源对象的性质。作为67牛的脑残粉之一,我在分析softmax的时候也先观察它最特化的形式,即只有一个分类的时候,这时softmax退化到logit函数:
当w=-30,b=20的时候,函数图像为:
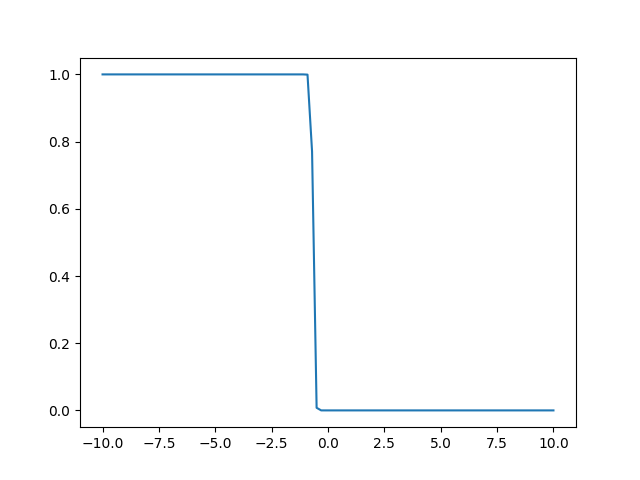
左边部分分类为1的概率十分接近1,右边十分接近0,logit函数有两个参数来控制