caculus of variations(施工中)
泛函是个啥?
泛函就是函数的函数,还记得我们当初学函数的时候,把函数比作一部机器,它的入料是一个变量,输出是一个函数值;而泛函这部“机器”,输入本身就是一部“机器”也就是函数,输出是泛函求值。用数学的语言讲,函数是一个映射:
$$
x_0\mapsto f(x_0)
$$
其中x_0叫做自变量,而泛函则是一个如下映射:
$$
f\mapsto f(x_0)
$$
其中
$$x_0$$
是一个参数。
变分法是个啥?
既然泛函是一个函数到数的映射,那么有些时候我们会对这个输出的数的极值感兴趣,变分法,是对于泛函求极值的一种方法,通过使用未知函数的积分与微分构造泛函,用来求未知函数泛函的极值。历史上比较经典的例子比如最速降线问题,一个小球从一个弯轨道的一段下落滑到另一端,使用哪种形状的轨道所用时间最短。因为轨道的形状不确定,所以小球划过每一小段轨道所用的时间也就不确定,对一个不确定的轨道上的运行时间作积分,这就成为了一个泛函。

变分法怎么玩?
对于某一特定函数\(y=f(x)\),我们可以先构造它的泛函\(J[y(x)]\),还是以最速降线为例,如果我们如下图建立坐标系,小球沿着轨道滑下:
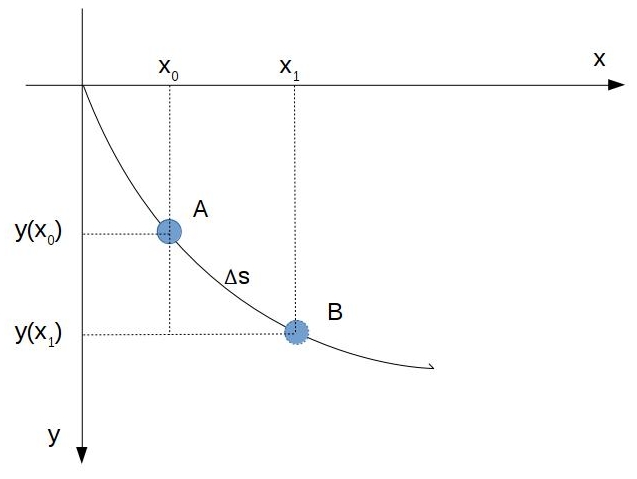
记从A到B小球滑动的这段轨道长度为\(ds\),根据勾股定理,我们可以求出\(ds\)的长度为
$$
ds = \sqrt{(x_1-x_0)^2+(y(x_1)-y(x_0))^2}
$$
$$
= \sqrt{dx^2-dy^2}
$$
$$
= \sqrt{1-y'(x_0)}dx
$$
那么小球从
$$ds$$
“左边”到“右边”滑动的时候,它的速度我们可以近似视为
$$
\newcommand{\pp}[2]{\frac{\partial #1}{\partial #2}}
\newcommand{\bb}{\pi R}
\newcommand{\bc}{\pi r}
$$
$$\frac{\partial A}{\partial t}$$
$$
J(\theta) = \frac 1 2 \sum_{i=1}^m (h_\theta(x^{(i)})-y^{(i)})^2
$$
The God said:
Let there be light
Thus:
$$
\nabla \cdot E = \frac{\rho}{\epsilon_0}
$$
$$
\nabla \cdot B =0
$$
$$
\nabla \times E = - \frac{\partial B}{\partial t}
$$
$$
\nabla \times B = \mu_0 J + \mu_0 \epsilon_0 \frac{\partial E}{\partial t}
$$