听ghost讲那最短路的事情之dijkstra算法
图论中的最短路算法,应该是每个进入图论的oier的入门课吧,虽然可能讲一节这个多此一举,但(为了凑数)还是说一说吧~
名称
dijkstra算法
属性
单源最短路算法、巨R眼镜(喂喂喂好像稍稍跑偏了啊……)
来历
在很久很久以前,互联网的规模还没发展到惊天地泣鬼神的时候,网络上的路由器依照静态路由表计算从一个节点(或网络)到另一个节点(或网络)的最短传包路径,就是用的dijkstra算法
思想
首先根据图的情况建立邻接矩阵,从出发点到各个节点的路径都有一个权值(没有道路直接相连置为+∞)如下图:
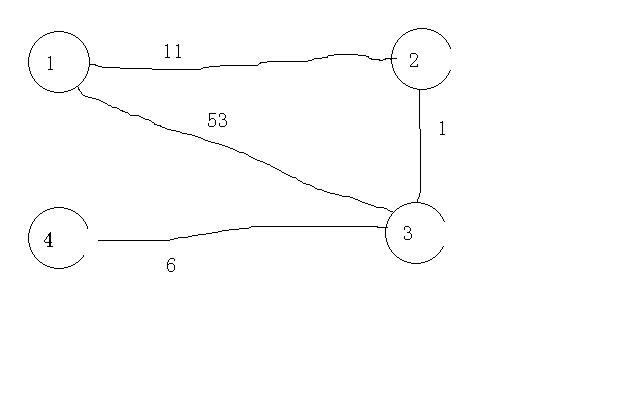
可建立邻接矩阵如下:
0 11 53 +∞
11 0 1 +∞
53 1 0 6
+∞ +∞ 6 0
接下来,寻找从节点1出发到各个其他节点的最短直连路,也就是从上面矩阵的第一行中找出(除了从一到一的那个0权回路以外的)最小值,当然,根据我超人的智慧已经提前你们找出来了,就是那个53!哇嘎嘎嘎……咳咳,言归正传,是那个从节点1到节点2的权为11的路径,此时,第一轮路径优化开始:把11那条路练的节点2当做从节点1侵略其他节点的“中继站”,看看“是从节点1直接到节点3权值(53)小呢”还是“以2为中继站倒一趟车再到节点3权值(12)小呢?”当然是12<53,现在把第一行第三列的53更新为12,也就是现在已知的从节点1到节点3的道路权值最小的是12;然后看能不能同理更新节点1到节点4的权值,不过可惜啊,两条路径都是正无穷权值,到节点4的权值没法更新了。接下来是第一轮路径优化的善后处理:把节点2置一个“已使用”标志,这样下一轮找中继站的时候就不会再找到节点2,这样的路径优化进行三遍后,临街矩阵的第一行就变了样子,也就是列出了从节点1到各个节点的最小权值:
0 11 12 18
这就是求最小权值的问题,如果要求再提高一点,想要求最短权值路径,就要在路径优化的时候多记一个数据,就是从节点1到被更新的点本轮使用的“中继站”是哪个节点,等输出的时候递归输出即可。
点评
dijkstra可谓图论最短路问题中资格最老也是最眼镜娘(循规蹈矩)的算法了,整个算法透着一股明显的贪心气息,是每个学习图论的oier居家旅行必备良方……
时间复杂度
O(n^2)因为路径优化进行了n-1(n是节点数)次,每次检查了n-1个节点是否能被更新路径。